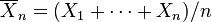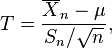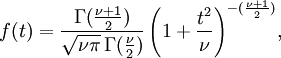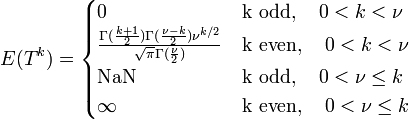توزیع تی استیودنت
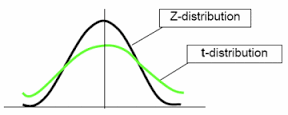
توزیع تی
در هنگام تعیین تقریبی میانگین نمونههای برداشته شده از یک متغیر تصادفی، توزیع تی-استودنت ( Student’s t-distribution) مطرح میشود. این توزیع اساس آزمونی به نام “تست تی” است که مقدار اطمینان از تفاوت دو متغیر تصادفی را از روی نمونههایشان اعلام میکند.
وجه تسمیه
فردی که برای اولین بار بر روی موضوع کار میکرد (ویلیام سیلی گوسه William Sealy Gosset)، گویا نمیتوانست به نام اصلیش مقالاتش را امضا کند و به ناچار از نام مستعار استیودنت (شاگرد) استفاده میکرد.
چگونگی ساخته شدن توزیع تی
…..
آزمون t
آزمون t ، توزیع یا در حقیقت خانوادهای از توزیعها است که با استفاده از آنها فرضیههایی را در باره نمونه در شرایط جامعه ناشناخته است، آزمون میکنیم. اهمیت این آزمون (توزیع) در آن است که پژوهشگر را قادر میسازد با نمونههای کوچکتر (حداقل ۲ نفر) اطلاعاتی در باره جامعه بدست آورد. آزمون t شامل خانوادهای از توزیعها است (برخلاف آزمون z) و اینگونه فرض میکند، که هر نمونهای دارای توزیع مخصوص به خود است، که شکل این توزیع از طریق محاسبه درجات آزادی (Degrees of Freedom) مشخص میشود. به عبارت دیگر توزیع t تابع درجات آزادی است و هر چه درجات آزادی (d.F) افزایش پیدا کند به توزیع طبیعی نزدیکتر میشود. هرچه درجات آزادی کاهش یابد، پراکندگی بیشتر میشود. خود درجات آزادی نیز تابعی از اندازه نمونه انتخابی هستند. هر چه تعداد نمونه بیشتر باشد بهتر است. از آزمون t میتوان برای تجزیه و تحلیل میانگین در پژوهشهای تک متغیری یک گروهی و دو گروهی و چند متغیری دو گروهی استفاده کرد.
فرض کنید که X1, …, Xn متغیرهای تصادفی مستقل نرمال با میانگین μ و واریانس σ۲ هستند.
اگر میانگین n نمونه فوق مقدار:
و واریانس آن :
باشند. میتوان به راحتی اثبات کرد که متغیر Z:
یک متغیر تصادفی نرمال با میانگین صفر و واریانس ۱ است.
حال به جای متغیر Z فوق، متغیر T را به صورت زیر تعریف میکنیم.
فرق این متغیر با Z، در این است که به جای  (مقدار واقعی واریانس) از مقدار تخمینی آن
(مقدار واقعی واریانس) از مقدار تخمینی آن 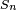 . استفاده شده است. میتوان نشان داد که متغیر T تابع توزیع احتمالی به فرم زیر دارد.
. استفاده شده است. میتوان نشان داد که متغیر T تابع توزیع احتمالی به فرم زیر دارد.
که ν (که درجه آزادی تابع است) برابر است با n − ۱ و Γ تابع گاما است.
تابع فوق را به صورت زیر نیز میتوان نگاشت:
که در آن B، تابع بتا است.
همانطور که دیده میشود، تابع توزیع نسبت به μ یا σ مستقل است.
ممانهای این تابع توزیع به صورت زیر هستند.
اگر ۰ < k < ν و k زوج باشد، با توجه به خواص تابع گاما، ممانها به صورت زیر ساده میشوند:
تست تی
برای بررسی این نکته که آیا میانگین نمونههای برداشته شده از یک متغیر تصادفی تا چه حد به میزان “واقعی” (که آزمایشگر نمیداند) نزدیک است از تست تی-استیودنت استفاده میشود.
- مثال: میانگین طول عمر ۱۵ بیمار سرطانی که داروی الف را مصرف کردند ۱۱۰ روز است با واریانس ۱۵. میانگین طول عمر ۱۵ بیمار دیگر که داروی مورد آزمایش را مصرف نکردند، ۱۰۰ روز گشته است با واریانس ۱۲. سوال: آیا بهبود در میانگین طول عمر بیمارانی که از داروی جدید استفاده کردند ناشی از عملکرد دارو است یا خطای میانگینگیری ناشی از تعداد محدود نمونهها؟
- جواب:
فرض صفر این مسئله را این قرار میدهیم که دارو اثری نداشته است. یا به عبارت دیگر میشود این طور فرض کرد که نمونههای برداشته شده از هر دو گروه، در واقع نمونهگیری از یک متغیر تصادفی است. در این مسئله، ما فرض صفر خود را هنگامی نقض میکنیم، که به احتمال ۹۵ درصد مطمئن شویم که غلط است. (این عدد اختیاری است)
این یک مسئله با ۱۴ درجه آزادی و دوطرفه است. پس از جدول مقادیر توزیع t، مقداری را که از تقاطع ۰.۹۷۵ درصد (مقادیر جدول از احتمال یک طرفه حاصل شدهاند) و ۱۴ درجه آزادی حاصل میشود را میابیم: ۲.۱۴۵. این مقدار را اگر در ورایانس اختلاف نمونهها ضرب کنیم (در محاسبه این واریانس فرض مستقل بودن را نیز کردهایم) و بر ریشه ۱۵ تقسیم کنیم عدد ۱۰.۵۸ حاصل میگردد.
پس به احتمال ۹۵ درصد، اگر دارو اثری نداشته باشد، باید اختلاف میانگین دو نمونه بین مثبت و منفی ۱۰.۵۸ باشد. که در این مثال هست. پس با قطعیت نمیتوان از اثر مثبت دارو صحبت کرد.
جدول مقادیر
توجه کنید که مقادیر این جدول از احتمال یک طرفه به دست آمدهاند. برای استفاده از آن در مسائل دوطرفه باید ابتدا مقدار احتمال را به یک طرفه تبدیل کنید. مثالا در ۹۰ درصد در احتمال دوطرفه، میشود ۹۵ درصد یک طرفه.
| ν | ۷۵٪ | ۸۰٪ | ۸۵٪ | ۹۰٪ | ۹۵٪ | ۹۷٫۵٪ | ۹۹٪ | ۹۹٫۵٪ | ۹۹٫۷۵٪ | ۹۹٫۹٪ | ۹۹٫۹۵٪ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ۱ | ۱٫۰۰۰ | ۱٫۳۷۶ | ۱٫۹۶۳ | ۳٫۰۷۸ | ۶٫۳۱۴ | ۱۲٫۷۱ | ۳۱٫۸۲ | ۶۳٫۶۶ | ۱۲۷٫۳ | ۳۱۸٫۳ | ۶۳۶٫۶ |
| ۲ | ۰٫۸۱۶ | ۱٫۰۶۱ | ۱٫۳۸۶ | ۱٫۸۸۶ | ۲٫۹۲۰ | ۴٫۳۰۳ | ۶٫۹۶۵ | ۹٫۹۲۵ | ۱۴٫۰۹ | ۲۲٫۳۳ | ۳۱٫۶۰ |
| ۳ | ۰٫۷۶۵ | ۰٫۹۷۸ | ۱٫۲۵۰ | ۱٫۶۳۸ | ۲٫۳۵۳ | ۳٫۱۸۲ | ۴٫۵۴۱ | ۵٫۸۴۱ | ۷٫۴۵۳ | ۱۰٫۲۱ | ۱۲٫۹۲ |
| ۴ | ۰٫۷۴۱ | ۰٫۹۴۱ | ۱٫۱۹۰ | ۱٫۵۳۳ | ۲٫۱۳۲ | ۲٫۷۷۶ | ۳٫۷۴۷ | ۴٫۶۰۴ | ۵٫۵۹۸ | ۷٫۱۷۳ | ۸٫۶۱۰ |
| ۵ | ۰٫۷۲۷ | ۰٫۹۲۰ | ۱٫۱۵۶ | ۱٫۴۷۶ | ۲٫۰۱۵ | ۲٫۵۷۱ | ۳٫۳۶۵ | ۴٫۰۳۲ | ۴٫۷۷۳ | ۵٫۸۹۳ | ۶٫۸۶۹ |
| ۶ | ۰٫۷۱۸ | ۰٫۹۰۶ | ۱٫۱۳۴ | ۱٫۴۴۰ | ۱٫۹۴۳ | ۲٫۴۴۷ | ۳٫۱۴۳ | ۳٫۷۰۷ | ۴٫۳۱۷ | ۵٫۲۰۸ | ۵٫۹۵۹ |
| ۷ | ۰٫۷۱۱ | ۰٫۸۹۶ | ۱٫۱۱۹ | ۱٫۴۱۵ | ۱٫۸۹۵ | ۲٫۳۶۵ | ۲٫۹۹۸ | ۳٫۴۹۹ | ۴٫۰۲۹ | ۴٫۷۸۵ | ۵٫۴۰۸ |
| ۸ | ۰٫۷۰۶ | ۰٫۸۸۹ | ۱٫۱۰۸ | ۱٫۳۹۷ | ۱٫۸۶۰ | ۲٫۳۰۶ | ۲٫۸۹۶ | ۳٫۳۵۵ | ۳٫۸۳۳ | ۴٫۵۰۱ | ۵٫۰۴۱ |
| ۹ | ۰٫۷۰۳ | ۰٫۸۸۳ | ۱٫۱۰۰ | ۱٫۳۸۳ | ۱٫۸۳۳ | ۲٫۲۶۲ | ۲٫۸۲۱ | ۳٫۲۵۰ | ۳٫۶۹۰ | ۴٫۲۹۷ | ۴٫۷۸۱ |
| ۱۰ | ۰٫۷۰۰ | ۰٫۸۷۹ | ۱٫۰۹۳ | ۱٫۳۷۲ | ۱٫۸۱۲ | ۲٫۲۲۸ | ۲٫۷۶۴ | ۳٫۱۶۹ | ۳٫۵۸۱ | ۴٫۱۴۴ | ۴٫۵۸۷ |
| ۱۱ | ۰٫۶۹۷ | ۰٫۸۷۶ | ۱٫۰۸۸ | ۱٫۳۶۳ | ۱٫۷۹۶ | ۲٫۲۰۱ | ۲٫۷۱۸ | ۳٫۱۰۶ | ۳٫۴۹۷ | ۴٫۰۲۵ | ۴٫۴۳۷ |
| ۱۲ | ۰٫۶۹۵ | ۰٫۸۷۳ | ۱٫۰۸۳ | ۱٫۳۵۶ | ۱٫۷۸۲ | ۲٫۱۷۹ | ۲٫۶۸۱ | ۳٫۰۵۵ | ۳٫۴۲۸ | ۳٫۹۳۰ | ۴٫۳۱۸ |
| ۱۳ | ۰٫۶۹۴ | ۰٫۸۷۰ | ۱٫۰۷۹ | ۱٫۳۵۰ | ۱٫۷۷۱ | ۲٫۱۶۰ | ۲٫۶۵۰ | ۳٫۰۱۲ | ۳٫۳۷۲ | ۳٫۸۵۲ | ۴٫۲۲۱ |
| ۱۴ | ۰٫۶۹۲ | ۰٫۸۶۸ | ۱٫۰۷۶ | ۱٫۳۴۵ | ۱٫۷۶۱ | ۲٫۱۴۵ | ۲٫۶۲۴ | ۲٫۹۷۷ | ۳٫۳۲۶ | ۳٫۷۸۷ | ۴٫۱۴۰ |
| ۱۵ | ۰٫۶۹۱ | ۰٫۸۶۶ | ۱٫۰۷۴ | ۱٫۳۴۱ | ۱٫۷۵۳ | ۲٫۱۳۱ | ۲٫۶۰۲ | ۲٫۹۴۷ | ۳٫۲۸۶ | ۳٫۷۳۳ | ۴٫۰۷۳ |
| ۱۶ | ۰٫۶۹۰ | ۰٫۸۶۵ | ۱٫۰۷۱ | ۱٫۳۳۷ | ۱٫۷۴۶ | ۲٫۱۲۰ | ۲٫۵۸۳ | ۲٫۹۲۱ | ۳٫۲۵۲ | ۳٫۶۸۶ | ۴٫۰۱۵ |
| ۱۷ | ۰٫۶۸۹ | ۰٫۸۶۳ | ۱٫۰۶۹ | ۱٫۳۳۳ | ۱٫۷۴۰ | ۲٫۱۱۰ | ۲٫۵۶۷ | ۲٫۸۹۸ | ۳٫۲۲۲ | ۳٫۶۴۶ | ۳٫۹۶۵ |
| ۱۸ | ۰٫۶۸۸ | ۰٫۸۶۲ | ۱٫۰۶۷ | ۱٫۳۳۰ | ۱٫۷۳۴ | ۲٫۱۰۱ | ۲٫۵۵۲ | ۲٫۸۷۸ | ۳٫۱۹۷ | ۳٫۶۱۰ | ۳٫۹۲۲ |
| ۱۹ | ۰٫۶۸۸ | ۰٫۸۶۱ | ۱٫۰۶۶ | ۱٫۳۲۸ | ۱٫۷۲۹ | ۲٫۰۹۳ | ۲٫۵۳۹ | ۲٫۸۶۱ | ۳٫۱۷۴ | ۳٫۵۷۹ | ۳٫۸۸۳ |
| ۲۰ | ۰٫۶۸۷ | ۰٫۸۶۰ | ۱٫۰۶۴ | ۱٫۳۲۵ | ۱٫۷۲۵ | ۲٫۰۸۶ | ۲٫۵۲۸ | ۲٫۸۴۵ | ۳٫۱۵۳ | ۳٫۵۵۲ | ۳٫۸۵۰ |
| ۲۱ | ۰٫۶۸۶ | ۰٫۸۵۹ | ۱٫۰۶۳ | ۱٫۳۲۳ | ۱٫۷۲۱ | ۲٫۰۸۰ | ۲٫۵۱۸ | ۲٫۸۳۱ | ۳٫۱۳۵ | ۳٫۵۲۷ | ۳٫۸۱۹ |
| ۲۲ | ۰٫۶۸۶ | ۰٫۸۵۸ | ۱٫۰۶۱ | ۱٫۳۲۱ | ۱٫۷۱۷ | ۲٫۰۷۴ | ۲٫۵۰۸ | ۲٫۸۱۹ | ۳٫۱۱۹ | ۳٫۵۰۵ | ۳٫۷۹۲ |
| ۲۳ | ۰٫۶۸۵ | ۰٫۸۵۸ | ۱٫۰۶۰ | ۱٫۳۱۹ | ۱٫۷۱۴ | ۲٫۰۶۹ | ۲٫۵۰۰ | ۲٫۸۰۷ | ۳٫۱۰۴ | ۳٫۴۸۵ | ۳٫۷۶۷ |
| ۲۴ | ۰٫۶۸۵ | ۰٫۸۵۷ | ۱٫۰۵۹ | ۱٫۳۱۸ | ۱٫۷۱۱ | ۲٫۰۶۴ | ۲٫۴۹۲ | ۲٫۷۹۷ | ۳٫۰۹۱ | ۳٫۴۶۷ | ۳٫۷۴۵ |
| ۲۵ | ۰٫۶۸۴ | ۰٫۸۵۶ | ۱٫۰۵۸ | ۱٫۳۱۶ | ۱٫۷۰۸ | ۲٫۰۶۰ | ۲٫۴۸۵ | ۲٫۷۸۷ | ۳٫۰۷۸ | ۳٫۴۵۰ | ۳٫۷۲۵ |
| ۲۶ | ۰٫۶۸۴ | ۰٫۸۵۶ | ۱٫۰۵۸ | ۱٫۳۱۵ | ۱٫۷۰۶ | ۲٫۰۵۶ | ۲٫۴۷۹ | ۲٫۷۷۹ | ۳٫۰۶۷ | ۳٫۴۳۵ | ۳٫۷۰۷ |
| ۲۷ | ۰٫۶۸۴ | ۰٫۸۵۵ | ۱٫۰۵۷ | ۱٫۳۱۴ | ۱٫۷۰۳ | ۲٫۰۵۲ | ۲٫۴۷۳ | ۲٫۷۷۱ | ۳٫۰۵۷ | ۳٫۴۲۱ | ۳٫۶۹۰ |
| ۲۸ | ۰٫۶۸۳ | ۰٫۸۵۵ | ۱٫۰۵۶ | ۱٫۳۱۳ | ۱٫۷۰۱ | ۲٫۰۴۸ | ۲٫۴۶۷ | ۲٫۷۶۳ | ۳٫۰۴۷ | ۳٫۴۰۸ | ۳٫۶۷۴ |
| ۲۹ | ۰٫۶۸۳ | ۰٫۸۵۴ | ۱٫۰۵۵ | ۱٫۳۱۱ | ۱٫۶۹۹ | ۲٫۰۴۵ | ۲٫۴۶۲ | ۲٫۷۵۶ | ۳٫۰۳۸ | ۳٫۳۹۶ | ۳٫۶۵۹ |
| ۳۰ | ۰٫۶۸۳ | ۰٫۸۵۴ | ۱٫۰۵۵ | ۱٫۳۱۰ | ۱٫۶۹۷ | ۲٫۰۴۲ | ۲٫۴۵۷ | ۲٫۷۵۰ | ۳٫۰۳۰ | ۳٫۳۸۵ | ۳٫۶۴۶ |
| ۴۰ | ۰٫۶۸۱ | ۰٫۸۵۱ | ۱٫۰۵۰ | ۱٫۳۰۳ | ۱٫۶۸۴ | ۲٫۰۲۱ | ۲٫۴۲۳ | ۲٫۷۰۴ | ۲٫۹۷۱ | ۳٫۳۰۷ | ۳٫۵۵۱ |
| ۵۰ | ۰٫۶۷۹ | ۰٫۸۴۹ | ۱٫۰۴۷ | ۱٫۲۹۹ | ۱٫۶۷۶ | ۲٫۰۰۹ | ۲٫۴۰۳ | ۲٫۶۷۸ | ۲٫۹۳۷ | ۳٫۲۶۱ | ۳٫۴۹۶ |
| ۶۰ | ۰٫۶۷۹ | ۰٫۸۴۸ | ۱٫۰۴۵ | ۱٫۲۹۶ | ۱٫۶۷۱ | ۲٫۰۰۰ | ۲٫۳۹۰ | ۲٫۶۶۰ | ۲٫۹۱۵ | ۳٫۲۳۲ | ۳٫۴۶۰ |
| ۸۰ | ۰٫۶۷۸ | ۰٫۸۴۶ | ۱٫۰۴۳ | ۱٫۲۹۲ | ۱٫۶۶۴ | ۱٫۹۹۰ | ۲٫۳۷۴ | ۲٫۶۳۹ | ۲٫۸۸۷ | ۳٫۱۹۵ | ۳٫۴۱۶ |
| ۱۰۰ | ۰٫۶۷۷ | ۰٫۸۴۵ | ۱٫۰۴۲ | ۱٫۲۹۰ | ۱٫۶۶۰ | ۱٫۹۸۴ | ۲٫۳۶۴ | ۲٫۶۲۶ | ۲٫۸۷۱ | ۳٫۱۷۴ | ۳٫۳۹۰ |
| ۱۲۰ | ۰٫۶۷۷ | ۰٫۸۴۵ | ۱٫۰۴۱ | ۱٫۲۸۹ | ۱٫۶۵۸ | ۱٫۹۸۰ | ۲٫۳۵۸ | ۲٫۶۱۷ | ۲٫۸۶۰ | ۳٫۱۶۰ | ۳٫۳۷۳ |
 |
۰٫۶۷۴ | ۰٫۸۴۲ | ۱٫۰۳۶ | ۱٫۲۸۲ | ۱٫۶۴۵ | ۱٫۹۶۰ | ۲٫۳۲۶ | ۲٫۵۷۶ | ۲٫۸۰۷ | ۳٫۰۹۰ | ۳٫۲۹۱ |
توزیع های مرتبط
- X˜t(ν) دارای توزیع تی است، اگر
 دارای توزیع عکس کایدو مقیاس شده بوده و
دارای توزیع عکس کایدو مقیاس شده بوده و  دارای توزیع نرمال باشد.
دارای توزیع نرمال باشد. - Y˜F(ν۱ = ۱,ν۲ = ν) دارای توزیع اف است اگر
 و
و 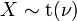 دارای توزیع تی-استودنت باشد.
دارای توزیع تی-استودنت باشد.  دارای توزیع نرمال است اگر
دارای توزیع نرمال است اگر 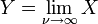 و X˜t(ν).
و X˜t(ν). - X˜Cauchy(0,1) دارای توزیع کوشی است اگر X˜t(ν = ۱).
| پارامترها | ν > 0 درجات آزادی (حقیقی) |
| گستره |  |
| تابع چگالی احتمال | 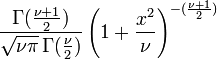 |
| تابع توزیع تجمعی(سیدیاف) | ![\begin{matrix} \frac{1}{2} + x \Gamma \left( \frac{\nu+1}{2} \right) \cdot\\[0.5em] \frac{\,_2F_1 \left ( \frac{1}{2},\frac{\nu+1}{2};\frac{3}{2}; -\frac{x^2}{\nu} \right)} {\sqrt{\pi\nu}\,\Gamma (\frac{\nu}{2})} \end{matrix}](http://upload.wikimedia.org/math/e/d/1/ed157c08d8dfcc5459aa89ad6db5f770.png) 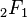 : تابع فوقهندسی : تابع فوقهندسی |
| میانگین | 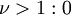 تعریف نشده برای بقیه مقادیر تعریف نشده برای بقیه مقادیر |
| میانه | ۰ |
| مُد | ۰ |
| واریانس |  تعریف نشده برای بقیه مقادیر تعریف نشده برای بقیه مقادیر |
| چولگی |  |
| کشیدگی | 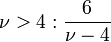 |
| انتروپی | ![\begin{matrix} \frac{\nu+1}{2}\left[ \psi(\frac{1+\nu}{2}) - \psi(\frac{\nu}{2}) \right] \\[0.5em] + \log{\left[\sqrt{\nu}B(\frac{\nu}{2},\frac{1}{2})\right]} \end{matrix}](http://upload.wikimedia.org/math/4/1/3/41353a2518872ce7c9ea9874ac8a243f.png)
|
| تابع مولد گشتاور (ام جی اف) | تعریف نشده |