بررسی توزیع داده ها
پس از جمع آوری داده ها از مشخصه های مورد مطالعه لازم است تا محقق بداند این داده ها از چه نوع توزیعی پیروی می کند.روشهای زیر در شناسایی نوع توزیع داده ها مورد استفاده قرار می گیرد:
1- نمودار همیستوگرام
تصویر زیر هیستوگرام متغیری است که از توزیع آماری نرمال پیروی میکند و نرمال بودن آن تایید شده است. در واقع محقق بعد از رسم نمودار هیستوگرام اگر مشاهده نمود که شکل هیستوگرام متقارن و دارای شکل زنگوله ای بوده است میتوان نرمالیتی آن را بپذیرد.
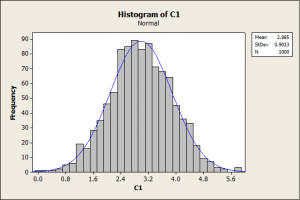
تصویر زیر هیستوگرام یک متغیر غیرنرمال می باشد. دو نمودار را با یکدیگر مقایسه نمایید.
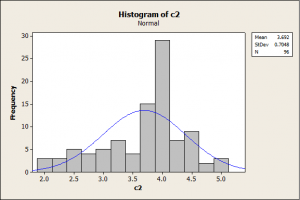
2- نمودار جعبه ای
یکی دیگر از روشهای گرافیکی و بصری تشخیص نوع توزیع داده ها استفاده از نمودار جعبه ای می باشد.اگر خط وسط نمودار جعبه ای در وسط جعبه قرار گیرید میتوان نرمال بودن آن تابع توزیع آن متغیر را تایید کرد.شکل زیر نمودار جعبه ای داده های یک متغیر نرمال می باشد.همانطور که مشاهده می کنید، خط تقریبا در وسط جعبه قرار گرفته است.
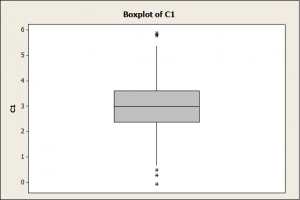
تصویر زیر نمودار جعبه ای یک متغیر غیرنرمال می باشد. دو نمودار را با یکدیگر مقایسه نمایید.همانطور که در تصویر زیر مشخص است خط کاملا در وسط جعبه قرار نگرفته و نشان می دهد که توزیع داده ها غیر نرمال می باشد.
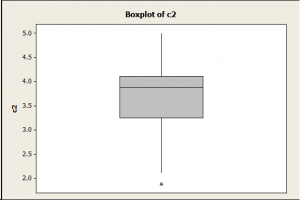
3-نمودار ppplot
نمودارهای p-p-plot و Q-Q-plot یکی دیگر از روشهای تشخیص نوع داده ها می باشد. در این روش هرچه نقاط ،خط ترسیم شده را بیشتر پوشش دهند توزیع داده ها بیشتر به توزیع نرمال نزدیکتر می شود.
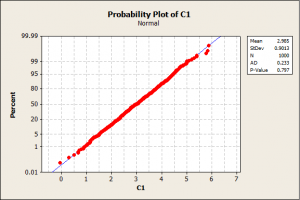
شکل زیر نمودار p-p-plot یک متغیر با توزیع نرمال می باشد.
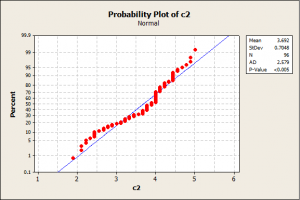
تصویر زیر نمودار p-p-plot یک متغیر غیرنرمال می باشد. دو نمودار را با یکدیگر مقایسه نمایید.همانطور که در تصویر زیر مشخص است خط خیلی خوب توسط نقاط(که بیانگر داده ها می باشد) پوشش داده نشده است و خیلی از نقاط بالا یا پایین خط قرار گرفته اند.
4- محاسبه چولگی و کشیدگی داده ها
ضرایب چولگی و کشیدگی در واقع میزان تخطی داده ها از توزیع داده ها را به محقق نشان می دهد و به زبان ساده میگوید که داده های جمع آوری شده تا چه اندازه از توزیع نرمال دور هستند. قدر مطلق ضريب چولگی و کشیدگی بزرگتر از 2 تخطي از نرمال بودن داده ها را نشان مي دهد. همچنین اگر مقدار خطای استاندارد ضریب چولگی و ضریب کشیدگی کوچکتر از 2- و یا بزرگتر از 2+ باشد؛ درآن صورت فرض نرمال بودن توزیع رد می شود.
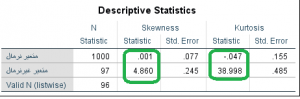
جدول زیر نتایج ضرایب چولگی و کشیدگی برای داده های یک متغیر نرمال و یک متغیر غیرنرمال را به تصویر کشیده است.همانطور که مشخص است توزیع داده های متغیر نرمال بین منفی 2 و مثبت 2 قرار گرفته ولی مقادیر چولگی و کشیدگی متغیر غیر نرمال بترتیب برابر 4.86 و 39.99 محاسبه شده است.
5- آزمون اندرسون دارلینگ
این آزمون دقیقترین و قوی ترین روش برای مطمئین شدن از نرمال بودن داده ها می باشد، چون تابع توزیع تجمعی تجربی مشاهدها را با تابع توزیع تجمعی نرمال مقایسه می کند.این آزمون در نرم افزار minitab گنجانده شده است.
6- آزمون کلموگروف اسمیرنف و آزمون شاپیرو ویلک
این دو آزمون پرکاربردترین روشهای بررسی نوع توزیع داده ها می باشد.فرض صفر در این آزمونها نرمال بودن توزیع داده ها و فرض مقابل آن عدم نرمال بودن توزیع داده ها می باشد.
سوال: راه حل برای داده های غیر نرمال چیست؟ آیا روشی وجود دارد که داده های غیر نرمال را به داده های نرمال تبدیل کنیم؟
در پاسخ به این سوال باید گفت که روشهای خوبی ارئه شده است که در زیر بصورت تیتروار به آنها اشاره کرده ایم.
1- روش تبدیل معکوس
2- روش لگاریتمی
3- روش ریشه دوم( جذر)
4-تبدیل باکس – کاکس(BOX-COX)
5-تبدیل جانسون(johnson Transformation)
منبع مطالب: کتاب کنترل کیفیت و تحلیل آماری با minitab16 نوشته دکتر مقصود امیری – مهندس شایان کرمی

